六、视觉伺服(Visual Servo)

定义：使用闭环控制环节中的计算机视觉数据来控制机器人运动。

分类：视觉伺服昆山伟创伺服电机、伺服驱动器核心代理商主要有两大模块，分别是基于位置的视觉伺服控制(Position-Based Visual Servoing)与基于图像的视觉伺服控制(Image-Based Visual Servoing)。

上图的流程只是一个IBVS执行周期的伪代码，实际的机械手是一个随动系统，将会一直运行上述过程。

1、PBVS

利用相机的参数建立图像信号与机器人的位置/姿态之间的映射关系，在伺服过程中，借助图像信号提取机器人的位置/姿态信息，并将它们与目标位置/姿态比较，形成闭环反馈控制。(这里不做详细介绍)

2、IBVS

将实时测量到的图像信号与目标位置/姿态的图像信号直接进行比较，利用所获得的图像误差进行闭环反馈控制。

根据不同的相机安装方式，IBVS也有两种不同的类型，(以电容插入PCB为例)，object(电容针脚)与target(孔洞)在图中的位置变化与否也不一样。

1)、eye in hand

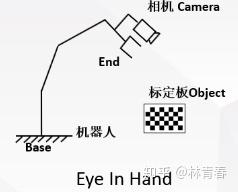
相机安装在机械手上，与机械手位置相对固定；

object电容绑定在tool上，相对于相机的位置不变；

target孔洞是图像视野中要去的目标位置，随着机械手移动而改变。

2)、eye to hand

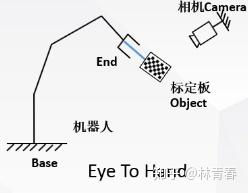
相机安装在机械手外的固定位置；

object电容绑定在tool上，在相机所拍的图片中位置是变化的；

terget孔洞是已经确定了的目标位置，因为相机位置固定，所以位置不变。(以上条件为假设PCB板放在固定的平台上，若PCB位于流水线上，则object与target都是位置可变化的实体)

3)、数学计算

• 补充：雅克比矩阵
  引用wiki百科对雅克比矩阵的定义：假设某个函数从R^n映射到R^m，雅克比矩阵就是R^n到R^m的线性映射，其重要意义在于它表现了一个多变数向量函数的最佳线性逼近。因此，雅可比矩阵类似于单变数函数的导数。
  $$\begin{gathered} F:R^n->R^m是一个从{\displaystyle n}维欧氏空间映射到到{\displaystyle m}维欧氏空间的函数。 \\ 这个函数由{\displaystyle m}个实函数组成:{\displaystyle y_1(x_1,\cdots ,x_n),\cdots ,y_m(x_1,\cdots ,x_n)}。 \\ 这些函数的偏导数(如果存在)可以组成一个m行n列的矩阵，为雅克比矩阵：{\displaystyle \left[\begin{array}{ccc}\frac{\mathrm{\partial }{y}_1}{\mathrm{\partial }{x}_1}& \cdots & \frac{\mathrm{\partial }{y}_1}{\mathrm{\partial }{x}_n}\\ ⋮& \ddots & ⋮\\ \frac{\mathrm{\partial }{y}_m}{\mathrm{\partial }{x}_1}& \cdots & \frac{\mathrm{\partial }{y}_m}{\mathrm{\partial }{x}_n}\end{array}\right].} \\ 此矩阵用符号表示为：{\displaystyle J_F(x_1,\dots ,x_n)}，或者{\displaystyle \frac{\mathrm{\partial }(y_1,\dots ,y_m)}{\mathrm{\partial }(x_1,\dots ,x_n)}.} \\ 这个矩阵的第{\displaystyle i}行是由梯度函数的转置{\displaystyle y_i(i=1,\cdots ,m)}表示的 \\ 如果{\displaystyle p}是{\displaystyle {\mathbb{R}}^n}中的一点，{\displaystyle F}在{\displaystyle p}p点可微分，根据数学分析，{\displaystyle J_F(p)}是在这点的导数。 \\ 在此情况下，{\displaystyle J_F(p)}这个线性映射即{\displaystyle F}在点{\displaystyle p}附近的最优线性逼近，也就是说当{\displaystyle x}足够靠近点{\displaystyle p}时， \\ 我们有{\displaystyle F(x)\approx F(p)+J_F(p)\cdot (x-p)} \end{gathered}$$
  

图像雅可比

分别设末端执行器的速度，图像特征点的变化速率分别为： $\stackrel{.}{\gamma },\stackrel{.}{f}$

图像雅可比是一个从末端执行器切线空间到图像特征切线空间的线性变换。

$\stackrel{.}{f}={\stackrel{.}{J}}_v(r)\stackrel{.}{\gamma }$

根据上述式子，建立了末端执行器pos与图像点之间的关系。下面通过更具体的实例来解释图像雅可比。

在基座标系统下，机械手末端运动的角速度与平移量分别为：

$$\begin{gathered} AngularVelocity{:}^c{\Omega }_e(t)={[{\omega }_x(t),{\omega }_y(t),{\omega }_z(t)]}^T \\ TranslationalVelocity{:}^c{T}_e(t)={[T_x(t),T_y(t),T_z(t)]}^T \end{gathered}$$

设点P在末端执行器上，其坐标为$P={[x,y,z]}^T$

机械手运动时，对点P求关于时间t的微分，得到： ${}^c\stackrel{.}{P}{=}^c{\Omega }_e{\times }^{c}P{+}^c{T}_e$

根据之前坐标概论中图像坐标与相机坐标的关系$\{\begin{array}{l}u=\frac{f\cdot X}{Z}\\ v=\frac{f\cdot Y}{Z}\end{array}$

即:

$式\mathrm{6.2.1}\{\begin{array}{l}x=\frac{uz}{f}\\ y=\frac{vz}{f}\end{array}$

对u,v求导数，X，Z都是函数，得到：

$式\mathrm{6.2.2}\{\begin{array}{l}\stackrel{.}{u}=f\cdot \frac{z\stackrel{.}{x}-x\stackrel{.}{z}}{z^2}\\ \stackrel{.}{v}=f\cdot \frac{z\stackrel{.}{y}-y\stackrel{.}{z}}{z^2}\end{array}$

根据速度的定义

$式\mathrm{6.2.3}\{\begin{array}{l}\stackrel{.}{x}=z{w}_y-y{w}_z+T_x\\ \stackrel{.}{y}=x{w}_z-z{w}_x+T_y\\ \stackrel{.}{z}=y{w}_x-x{w}_y+T_z\end{array}$

将式式6.2.1带入=>式6.2.3，得到：

$式\mathrm{6.2.4}\{\begin{array}{l}\stackrel{.}{x}=z{w}_y-\frac{vz}{f}{w}_z+T_x\\ \stackrel{.}{y}=\frac{uz}{f}{w}_z-z{w}_x+T_y\\ \stackrel{.}{z}=\frac{z}{f}(v{w}_x-u{w}_y)+T_z\end{array}$

将式式6.2.2带入=>式6.2.4，得到：

$\{\begin{array}{l}\stackrel{.}{u}=\frac{f}{z}{T}_x-\frac{u}{z}{T}_z-\frac{uv}{f}{w}_x+\frac{f^2+u^2}{f}{w}_y-v{w}_z\\ \stackrel{.}{v}=\frac{f}{z}{T}_y-\frac{v}{z}{T}_z+\frac{uv}{f}{w}_y-\frac{f^2+u^2}{f}{w}_x+u{w}_z\end{array}$

用矩阵表示：

$\left[\begin{array}{c}\stackrel{.}{u}\\ \stackrel{.}{v}\end{array}\right]=\left[\begin{array}{cccccc}\frac{f}{z}& 0& -\frac{u}{z}& -\frac{uv}{f}& \frac{f^2+u^2}{f}& -v\\ 0& \frac{f}{z}& -\frac{v}{z}& -\frac{f^2+u^2}{f}& \frac{uv}{f}& u\end{array}\right]\left[\begin{array}{c}{T}_x\\ T_y\\ T_z\\ w_x\\ w_y\\ w_z\end{array}\right]$

上式反映了某点在图像坐标系下与相机坐标系下运动之间的关系

计算末端执行器速度

先前实例说明了使用机器手末端执行器动作计算相机坐标系的数据。然而，视觉伺服昆山伟创伺服电机、伺服驱动器核心代理商控制通常需要r给定f的反馈计算作为输入。雅可比矩阵为k行m列，使用图像雅可比计算末端执行器速度，需要考虑两种情况：

当

$x==m$ ，J为奇异矩阵，J逆存在

$\stackrel{.}{\gamma }=\stackrel{.}{J}{}_v(r{)}^{-1}\cdot \stackrel{.}{f}$

当 $x\ne m$ ，J逆不存在，假设J满秩，计算最小二乘解

$$\begin{gathered} \stackrel{.}{\gamma }=\stackrel{.}{J}{}_v^{+}(r)\cdot \stackrel{.}{f}+（I-J{}_v^{+}(r)\cdot J{}_v^{}(r))b \\ J{}_v^{+}(r)是J{}_v^{(}r)的伪逆，b是适合维度的任意向量 \end{gathered}$$

伺服任务

在这节中，我们将回顾一些问题，并且提出基于图像的解决方法。在所有案例中，我们都假设两个相机的场景都能解决这些问题。

a、点到点(Point to Point)

假设有一点P要去到期望的目的点S，两个相机都在观测同一个场景，P和S都在一个工作空间的充要条件是P和S都在每张图像中。假设点P在左右两个相机拍摄的图像中坐标为：

${[u^t,v^t]}^T,{[u^r,v^r]}^T$

则设

$$\begin{gathered} f={[u^t,v^t,u^r,v^r]}^T \\ T=R^3 \\ (F为T到R^4的映射) \end{gathered}$$

同时假设S在左右两个相机拍摄的图像中坐标为：$f_d={[u_s^t,v_s^t,u_s^r,v_s^r]}^T$

于是有:$e_{pp}(f)=f-f_d$

这个问题的图像雅可比行列式可以通过每个摄像机的“堆叠”来构建，同时要注意，必须为每个摄像机使用坐标变换，以便将摄像机坐标中的末端执行器速度与机器人参考系相关联。

但是，计算出来的结果雅可比矩阵为4行6列秩为3，不能求逆。两个相机提供了四个参数，观测点只有三个自由度，于是，有一个参数是多余的，或者等效地，观察被约束为位于四维测量空间的三维子空间上，这种约束为立体视觉中的极线约束。

有很多种方法求解极线约束问题，其中，最简单的是要注意大多数立体摄像系统的排列使得摄像机x（水平）轴大致共面。在这种情况下，冗余信息主要集中在y（垂直）坐标上，因此可以丢弃。 这样做会从雅可比行列中删除一行，并且生成的矩阵具有明确定义的逆矩阵。

b、点到线(Point to Line)

假设点P在机械手末端，要移动到到点S1与S2组成的线段上，要求双目视觉都能看到这个工作空间。

$P:[u^l,v^l],S1:[u_1^l,v_1^l],S2:[u_2^l,v_2^l]$

根据小孔成像原理，如果从左相机原点到这三个点所成向量共面，则这三个点在图像上共线，于是，构建标量三重积(scalar triple product)：

$e_{pl}^l([u^l,v^l{]}^T)=(\left[\begin{array}{c}{u}_1^l\\ v_1^l\\ f\end{array}\right]\times \left[\begin{array}{c}{u}_2^l\\ v_2^l\\ f\end{array}\right])\cdot \left[\begin{array}{c}{u}^l\\ v^l\\ f\end{array}\right]$

对右相机进行同样的处理，得到：

$e(f)=\left[\begin{array}{c}{e}_{pl}^l([u^l,v^l{]}^T)\\ e_{pl}^r([u^r,v^r{]}^T)\end{array}\right],f=[u^l,v^l,u^r,v^r]$

f是点P在图像坐标下的线性投影，雅可比也是图像雅可比对于点P的线性变化。为了明确这一点，则有:

$J_{pl}^l(u_1^l,v_1^l,u_2^l,v_2^l,u^l,v^l)=(\left[\begin{array}{c}{u}_1^l\\ v_1^l\\ f\end{array}\right]\times \left[\begin{array}{c}{u}_2^l\\ v_2^l\\ f\end{array}\right]{)}^T\left[\begin{array}{c}{J}_p^l(P)\\ 0\end{array}\right]$

$$\begin{gathered} 完整雅可比行列式是由J_{pl}^l和J_{pl}^r组成的“堆叠”乘以坐标变换， \\ 以将机器人坐标中的末端执行器速度与摄像机坐标系中的等效运动相关联。 \end{gathered}$$

加入给定了末端执行器上的第二个点，能够通过简单的两个PL和他们的图像雅可比定义一个四自由度的位置操作，同样地，在执行器上再选择一个世界坐标点，设置额外的一个PL问题就拓展为六自由度的定位问题。

江苏和讯自动化设备有限公司成立于2012年，注册资本1000万元。公司是集研发、项目设计、销售、维修、工控自动化培训为一体的专业自动化公司。是veichi伟创总代理、kinco步科核心代理，主营销售：伟创变频器、伟创伺服、伟创PLC、伟创行业专机、步科触摸屏、步科步进电机、步科伺服、步科低压伺服、步科PLC、步科变频器等产品，凭借优惠的价格和专业的售后服务获得合作伙伴的广泛好评，欢迎来电咨询。

感谢您访问昆山伟创总代理、步科核心代理网站，我们会为您提供优质的服务。